In converting the equation to a divergence, we have modified the interface conditions.  The natural boundary condition for each component equation of (2.10) is now the normal component of the argument of the divergence:
(2.11)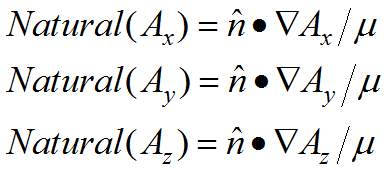  

The default interior interface condition assumes component-wise continuity of the surface terms across the interface.

Of the conditions (2.2) required by Maxwell’s equations at an interface, the first describes the tangential components of , which by (2.3) involve the normal components of .  Eq. (2.11) shows that these components scale by , satisfying the tangential condition on .

The second condition is satisfied by the fact that the variables have only a single representation on the boundary, requiring that their tangential derivatives, and therefore the normal component of , will be continuous across the interface.

In all cases it is important to keep the attached to the term to preserve the correct interface jump conditions.