Technical Notes > Applications in Electromagnetics

I. Maxwell's Equations

The purpose of this note is to develop formulations for the application of FlexPDE to various problems in electromagnetics. It is not our intention to give a tutorial on electromagnetics; we assume that the reader has some familiarity with the subject, and has access to standard references.

The starting point for our discussion is, as usual, Maxwell's equations:

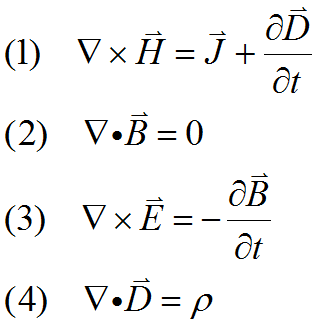
To these we add the constitutive relations

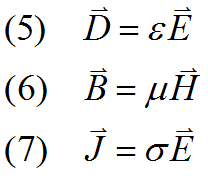
(In isotropic materials, , and are scalars, possibly nonlinear. In more complex materials, they may be tensors. In studies involving hysteresis or permanent magnets, modifications must be made to equation (6))

From these can be derived a convenient statement of charge conservation:

These equations form a very general framework for the study of electromagnetic fields, and admit of numerous combinations and permutations, depending on the characteristics of the problem at hand. Much confusion arises, in fact, from the tendency of textbooks to specialize the equations too soon, in order to simplify the exposition. This approach appears to present as a generally applicable formulation one which in reality embodies many assumptions about the problem being analyzed. We will discover that some alterations or substitutions that seem esthetically pleasing will not turn out to be wise computationally.

II. Choice of variables

A constraint due directly to the Finite Element model used in FlexPDE strikes us at the very outset. FlexPDE uses a continuous piecewise polynomial representation of all model variables. That is, at each computational node in the system it is assumed that each variable takes on a unique value, and that these nodal values can be connected in space by polynomial interpolations.

Application of the Divergence Theorem and Stokes' Theorem to Maxwell's equations yield the following boundary rules at material interfaces.

•The tangential component of is continuous; the normal component of is continuous (in the absence of surface charges).

•The tangential component of is continuous (in the absence of surface current); the normal component of is continuous.

These rules are in general inconsistent with the model assumptions of FlexPDE. This means that the field components themselves cannot be chosen as the model variables unless one of the following conditions applies:

• There are no material property discontinuities in the domain,

• The discontinuous components of the field are absent in the specific configuration being modeled.

For example, if we know that in a specific configuration that all the electric fields must be tangential to the material interfaces, we can use as a model variable. If we know instead that all the electric fields are normal to the material interfaces, we can use as a model variable.

The analysis of fields in terms of the field components comprises the bulk of textbook treatments, and we will not pursue the topic further here. We will instead turn our attention to a more generally applicable modeling approach. Nevertheless, despite the seemingly restrictive nature of these prohibitions, there is a large class of problems which can be analyzed successfully by FlexPDE in terms of field components.

III. Potentials

For any twice-differentiable vector , the vector identity holds. This identity together with equation (2) implies that we can define a vector potential function , the magnetic vector potential, such that

A theorem due to Helmholtz states that a vector field can be uniquely defined only by specifying both its curl and its divergence. We must remain aware, therefore, that at this point our vector potential is incompletely determined. The arbitrariness of is frequently exploited to simplify the equations. In many cases, it is not necessary to explicitly specify , allowing the boundary conditions and the artifacts of the computational model to define it by default.

Substituting relation (9) into equation (3) gives . Another vector identity states that for any twice differentiable scalar . This allows us to define a scalar potential function such that

In the absence of time variation, is seen to be the electrostatic potential.

Application of Faraday's Law to a pillbox on a material interface shows that V must be continuous across material interfaces. Application of Stokes' Theorem to shows that the tangential component of must be continuous across material interfaces. All the conventional definitions of also have the property that the normal component of is continuous across material interfaces. Therefore, formulations in terms of and completely satisfy the modeling assumptions of FlexPDE.

Since the two definitions (9) and (10) satisfy equations (2) and (3), we are left with Maxwell's equations (1) and (4), which in terms of and are:

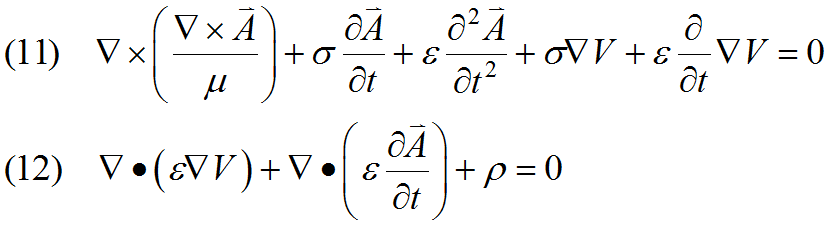
At this point, it is customary in the literature to apply vector identities to convert the 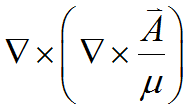into a form containing , so that a complete definition of can be achieved. In fact, these transformations require that be continuous across material interfaces. We therefore defer this operation for discussion under the appropriate specializations to follow. We should also point out that in (11) we have substituted , a substitution we may later wish to rescind.

IV. Boundary Conditions

FlexPDE uses the Divergence Theorem and its related Curl Theorem to reduce the order of second derivative terms, and assumes that the resulting surface integrals vanish at internal boundaries. Applied to (12), this process results in the continuity of the normal component of, as required by boundary rule 1). Applied to (11), this process results in the continuity of the tangential component of , as required by boundary rule 2).

At exterior boundaries, the Natural boundary condition specifies the value of the integrand of the surface integrals. For equation (11) this means the tangential component of , while for equation (12) it means the normal component of.

1. Symmetry planes

Following the above definition of the natural boundary condition, the specification "NATURAL(V)=0" for equation (12) means that the normal component of is zero. This means that field lines must be parallel to the system boundary and that potential contours must be normal to the boundary. These are the conditions of a symmetry plane.

Similarly, if we specify "NATURAL(A)=0" for equation (11), we require that the tangential component of be zero. This says that field lines and potential contours must be normal to the boundary, which is again the condition of a symmetry plane.

2. Perfect conductors

Since a perfect conductor cannot sustain a field, the boundary condition "VALUE(V)=constant" for equation (12) defines a perfectly conducting boundary. Note that since equation (12) contains only derivatives of V, an arbitrary constant value may be added to the solution without affecting the equation. In order for a numerical solution to succeed, there must be some point in the domain at which a value condition is prescribed, in order to make the potential solution unique.

Similarly, the specification "VALUE(A)=constant" for equation (11) forces the normal component of to be zero. As with V, a value should be ascribed to somewhere in the domain, in order to make the potential solution unique.

3. Distant Boundaries

Ampere's Law states that the integral of around a closed path is equal to the integral of over the enclosed surface, or just I, the enclosed current. Now, is the tangential component of , which is exactly the quantity specified in equation (11) by the Natural boundary condition. In many cases, this fact can be used to construct meaningful terminating boundary conditions for otherwise open domains.

The differential form of Ampere's Law can also be used to derive a general rule for the value of :

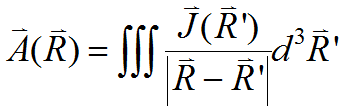
(In time-varying systems, must refer to a current retarded in time by the propagation time from to .)

This form has the property that . We may add to this definition the gradient of an arbitrary scalar function G without affecting the resulting fields.

At points distant from any currents we may write

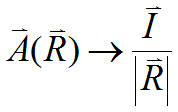Note that here is a vector which embodies the direction of the current, and that has the direction of .

V. Harmonic Analysis

Equations (11) and (12) describe a full time dependent model of the fields, which can be extremely expensive to compute. In many cases of interest, the time dependence we desire to study is the stable oscillation caused by a sinusoidal excitation. In these cases it is convenient to make the assumption that each of the field components can be expressed in the complex form

Where is any of the field quantities, is an associated complex amplitude (a function of space only),

is the angular velocity, and is the square root of minus 1. The observable field quantity is then the real part of P, Re(P).

With these assumptions, the time derivative terms in our equations reduce to simple forms:

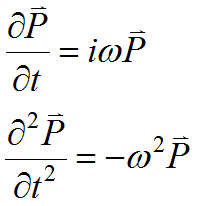
Applying these assumptions to equations (11) and (12) results in the harmonic equations

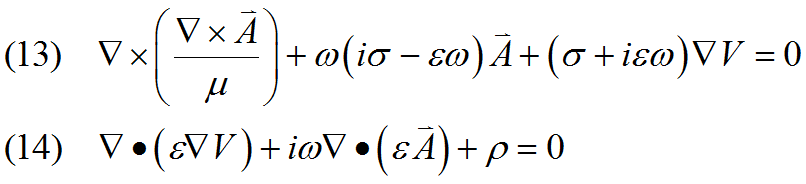
These equations require solution in space only, and are thus much more economical than the full time dependent system (11), (12). We will return to these equations frequently in the sections which follow.

VI. Posing Equations for FlexPDE

We have been writing our equations in terms of vector fields, but in fact FlexPDE is not able to deal directly with vector fields; we must manually reduce the system to component equations. In a three dimensional space, equation (11) comprises three component equations while equation (12) is scalar. So we have a total of four equations in four unknowns, Ax, Ay, Az and V.

Equations (13)-(14) are more complicated, since each component has a real and an imaginary part, for a total of eight components. Each of these eight scalar variables must be represented by a separate component equation.

We will not expand the equations into their final form just yet, because in most of the specializations addressed subsequently the resulting forms are not nearly so frightening as the full equations.

VII. Specializations

In most problems of interest, the full generality of equations (11) and (12) or their harmonic equivalents (13) and (14) are not necessary. Analysis of the needs of the problem at hand can usually lead to considerable simplification. We will consider a few cases here.

1. Electrostatics

For fields which are constant in time, equation (12) decouples from equation (11), and the electric scalar potential may be found from the single equation

Since FlexPDE applies the divergence theorem over each computational cell, inclusion of inside the divergence is sufficient to guarantee the correct behavior of the field quantities across material interfaces. The natural boundary condition on V becomes a specification of the normal derivative of .

2. Magnetostatics

For fields which are constant in time, equation (11) becomes

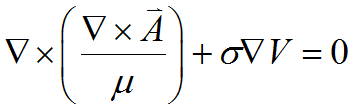
Here the term s Grad(V) is in fact a representation of the current density , which we will probably wish to specify directly as the driving current for the fields:

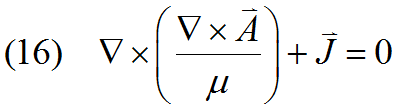
In the geometric interpretation of , for which, has components parallel to the components of , so if is restricted to a single component, we may restrict to only that component.

As discussed in section IV, the Natural boundary condition for specifies the tangential component of . Natural()=0 specifies a symmetry plane, and Value()=0 specifies a perfect conductor.

3. Non-magnetic Materials (constant )

In the common case where is constant, we can perform some simplification on equation (11). We can apply the vector identity

To give

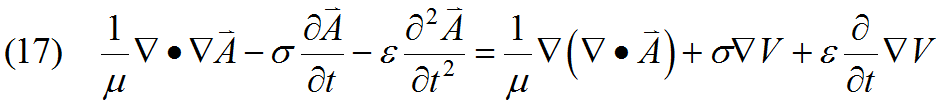Since we now have an explicit , we are in a position to define it in any way we choose to generate a form appropriate to our needs. The definition of is commonly known as the "Gauge Condition". The choice of gauge will be determined by what it is that we know about the problem at hand. Several common gauge conditions and the resulting forms of (11)-(12) are given below.

Note that this operation is not without consequences. The definition of the natural boundary condition has changed. It is no longer the boundary value of , but is now the boundary value of . Natural()=0 remains the condition for a symmetry plane, and Value()=0 still defines a perfect conductor boundary, but care must be taken if other values are assigned. In the case , the two will be equivalent, in other choices of gauge they may not be.

Also note that because of typographical constraints we have written for the component-wise Laplacian of the vector . This notation is not strictly correct in curvilinear coordinates, and a more careful derivation must be made in those cases.

Without making further assumptions about or , we can apply the Coulomb gauge condition, .

With this assertion, equation (17) becomes

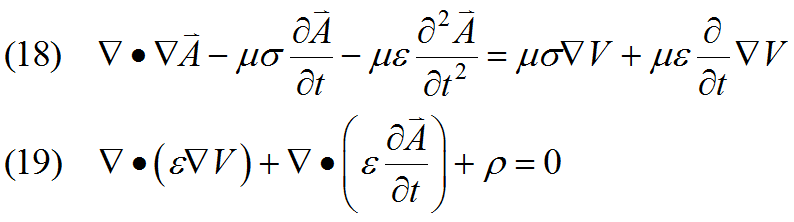
Note that even though we have assumed, we are not free to delete the 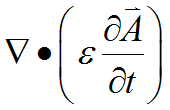from equation (18) unless is also constant. Piecewise constancy of is not sufficient, because is undefined at the interface and we have no way to apply a divergence theorem to convert it to a surface integral.

4. Non-magnetic Materials with constant

In the special case where both and are constant, the scalar potential equation (19) with Coulomb gauge can be simplified to

Alternatively, we can use the "Diffusion" gauge condition:

We can reverse the order of differentiation and cause to cancel the term in equation (11) and replace the term in equation (12)

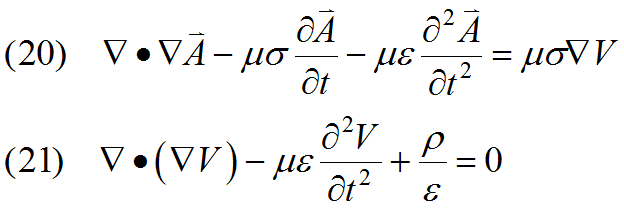
In some cases, s Grad(V) may be interpreted as the negative of the static current density, in which case the equations decouple and (20) may be eliminated.

5. Non-magnetic Materials with constant and

In the special case where , and are all constant, we can use the Lorentz gauge condition:

This allows all the V terms to cancel from equation (17) resulting in decoupled equations for and V

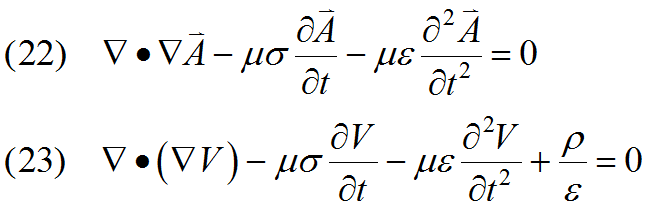
The equations have now been decoupled, and may be solved separately. These forms are useful in the solution of wave propagation problems.

VIII. Specializations of the Harmonic Equations

1. Non-magnetic Materials

Equations (13) and (14) can also be specialized to the case of constant . The basic form of equation (13) is

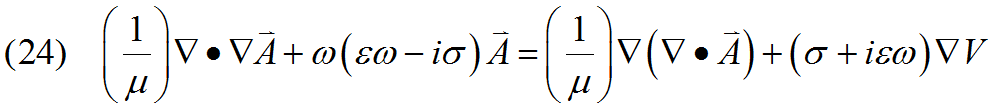
Without making further assumptions about or we may apply the Coulomb gauge condition

from which equations (13) and (14) become

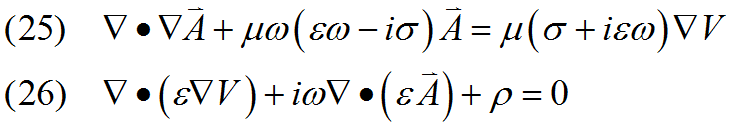
Note that even though we have assumed , we are not free to delete the from equation (26) unless is constant.

2. Non-magnetic Materials with constant

In the special case where both and are constant, equation (26) with Coulomb gauge can be simplified to

Alternatively, we can use the diffusion gauge condition

from which we derive the equations

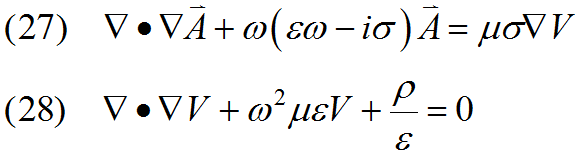
In some cases,may be interpreted as the negative of the conduction current density, in which case the equations decouple and (28) may be eliminated.

3. Non-magnetic Materials with constant e and s

In the special case where , and are all constant, we can use the Lorentz gauge condition,

which in the harmonic approximation becomes

All the V terms vanish in equation (24), and the pair (13), (14) become

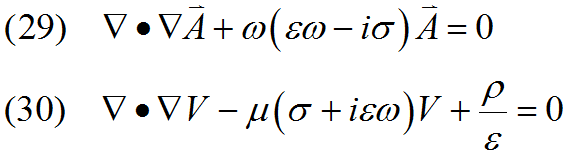
The equations have now been decoupled, and may be solved separately. These forms are useful in the solution of wave propagation problems.