In two dimensional geometry with a single nonzero component of , the gauge condition is automatically satisfied.  Direct application of eq. (2.4) is therefore well posed, and we can proceed without further modification.

In 3D, however, direct implementation of eq. (2.4) does not impose a gauge condition, and is therefore ill-posed in many cases.  One way to address this problem is to convert the equation to divergence form using the vector identity
(2.6)     .

As long as is piecewise constant we can apply (2.6) together with the Coulomb gauge to rewrite (2.4) as
(2.7)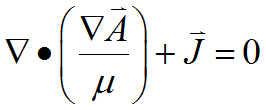    

If is variable, we can generalize eq. (2.6) to the relation
(2.8)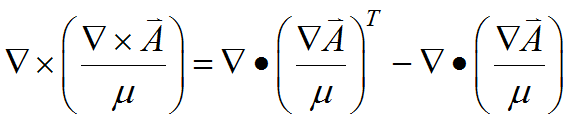    

We assert without proof that there exists a gauge condition which forces
(2.9)     .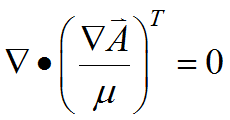

The equations governing can be stated as

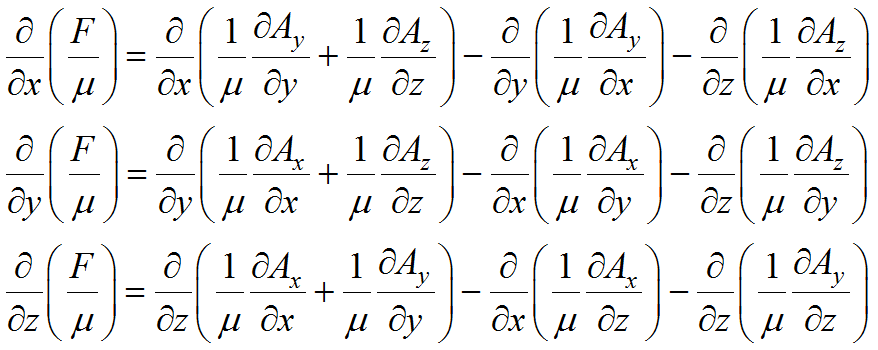
It is not necessary to solve these equations; we show them merely to indicate that embodies the commutation characteristics of the system.  The value of is implied by the assertion (2.9).  Clearly, when is constant, the equations reduce to , for which is a solution.

Using the definition (2.9) we can again write the divergence form
(2.10)     .