User Guide > Moving Meshes > The Pulsating Blob

Using the position balancing form from the preceding paragraph, the modified script for our example problem becomes:

TITLE 'Heat flow around an Insulating blob'

VARIABLES

Phi { the temperature }

Xm = MOVE(x) { surrogate X }

Ym = MOVE(y) { surrogate Y }

DEFINITIONS

K = 1 { default conductivity }

R0 = 0.75 { initial blob radius }

EQUATIONS

Phi: Div(-k*grad(phi)) = 0

Xm: div(grad(Xm)) = 0

Ym: div(grad(Ym)) = 0

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0 VELOCITY(Xm)=0 VELOCITY(Ym)=0

LINE TO (1,-1)

NATURAL(Phi)=0 LINE TO (1,1)

VALUE(Phi)=1 LINE TO (-1,1)

NATURAL(Phi)=0 LINE TO CLOSE

REGION 2 'blob' { the embedded blob }

k = 0.001

START 'ring' (R,0)

VELOCITY(Xm) = -0.25*sin(t)*x/r

VELOCITY(Ym) = -0.25*sin(t)*y/r

ARC(CENTER=0,0) ANGLE=360 TO CLOSE

TIME 0 TO 2*pi

PLOTS

FOR T = pi/2 BY pi/2 TO 2*pi

GRID(x,y)

CONTOUR(Phi)

VECTOR(-k*grad(Phi))

ELEVATION(Phi) FROM (0,-1) to (0,1)

ELEVATION(Normal(-k*grad(Phi))) ON 'ring'

END

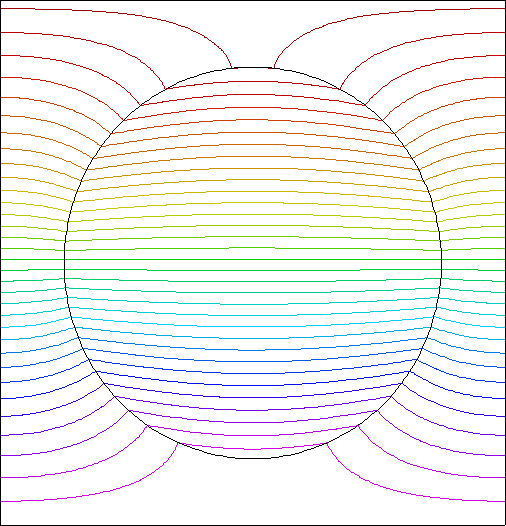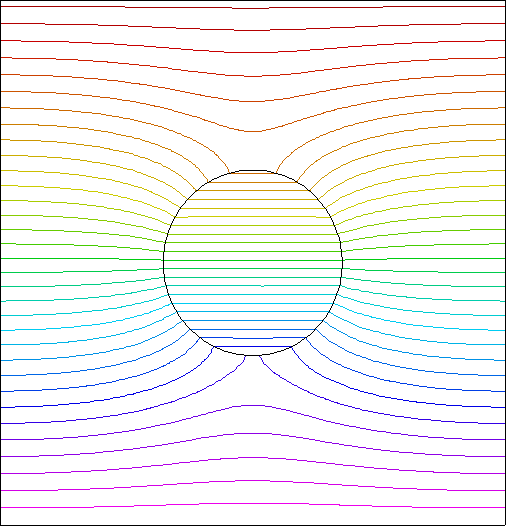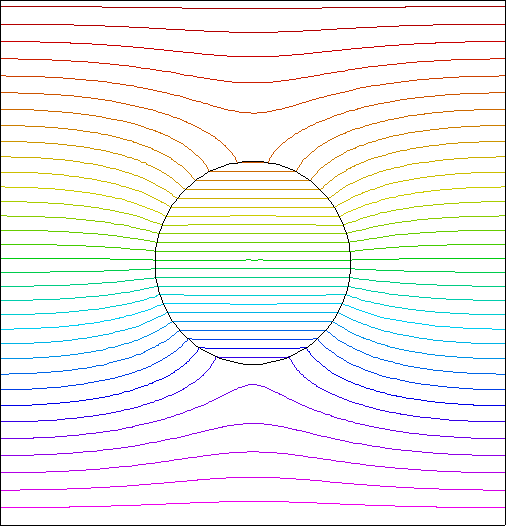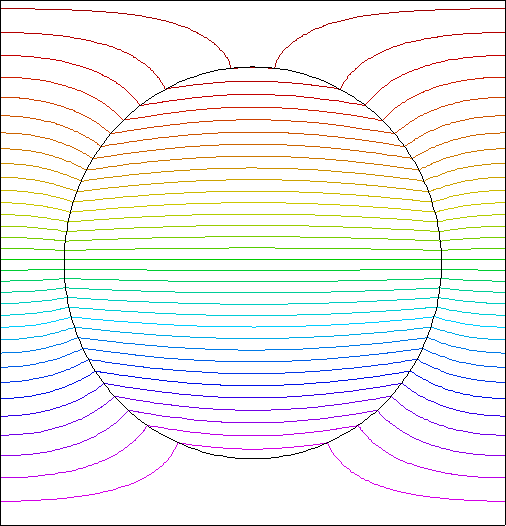
The position and velocity forms of this problem can be seen in the following examples:

Three-dimensional forms of the problem can be seen in the following examples: