<< Click to Display Table of Contents >> Navigation:  User Guide > Vector Variables > Magnetic Vector Potential

Our Cylindrical torus problem can easily be converted to a model of a current-carrying torus inside a box.

The geometry is unchanged, but we now solve for the magnetic vector potential A.  We will also move the location slightly outward in radius to avoid the singularity at R=0.

Maxwell's equation for the magnetic field can be expressed in terms of the magnetic vector potential as

Curl(Curl(A)/mu) = J

Here J is the vector current density and mu is the magnetic permeability.

The script becomes

TITLE 'Magnetic Field around a Current-Carrying Torus'

COORDINATES YCYLINDER                { implicitly R,Z,Phi }

VARIABLES

A = VECTOR(0,0,Aphi)                

DEFINITIONS

J = VECTOR(0,0,0)        { default current density }

mu = 1

Rad = 0.5                        { blob radius (renamed)}

EQUATIONS

A: CURL(CURL(A)/mu)) = J

BOUNDARIES

REGION 1 'box'

START(1,-1)

VALUE(A)=VECTOR(0,0,0)        

LINE TO (3,-1) TO (3,1) TO (1,1) TO CLOSE

REGION 2        'blob'        { the torus }

J = VECTOR(0,0,1)        { current in the torus }

START 'ring' (2,Rad)

ARC(CENTER=2,0) ANGLE=360 TO CLOSE

PLOTS

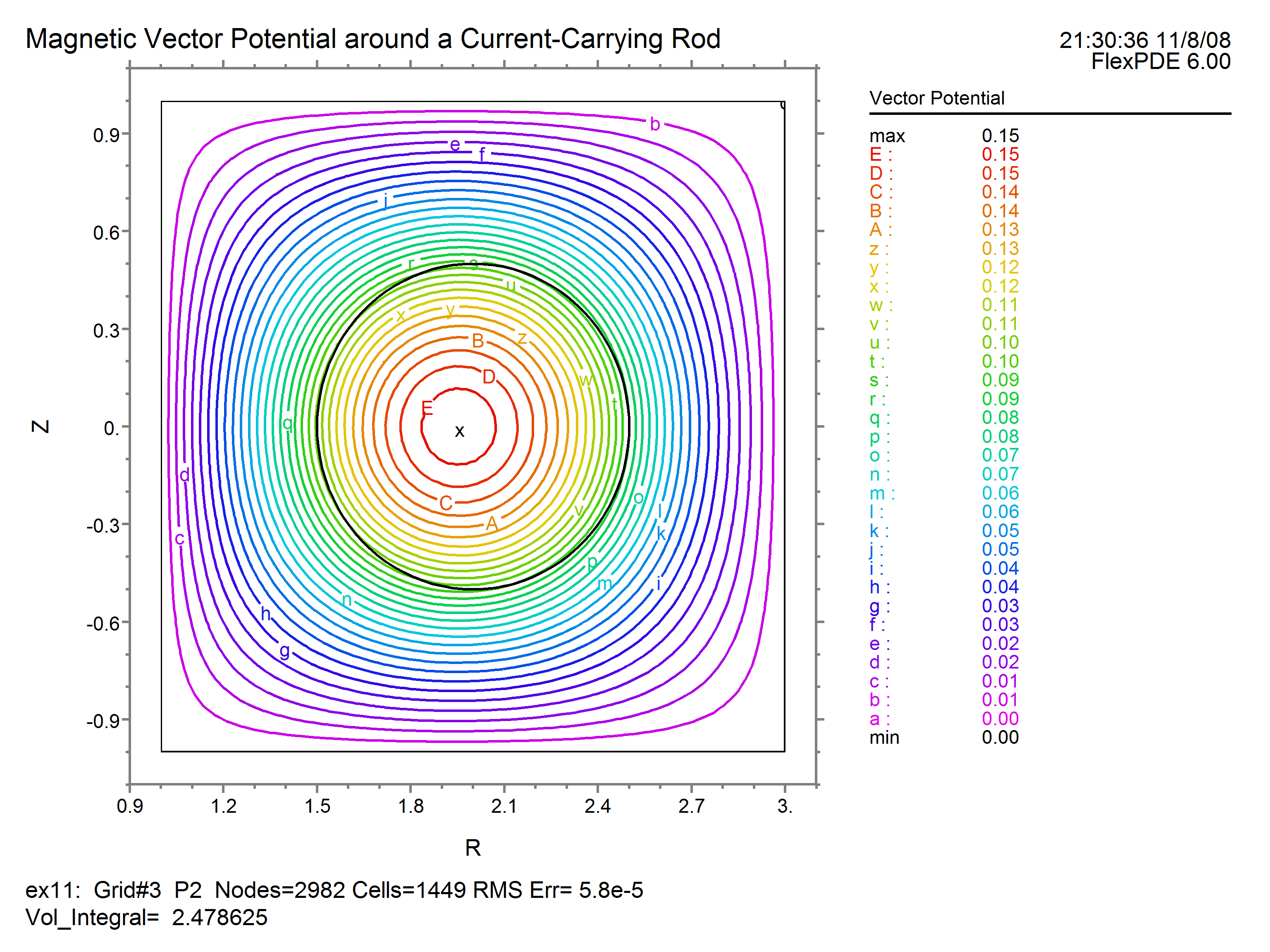
CONTOUR(Aphi) as "Vector Potential"

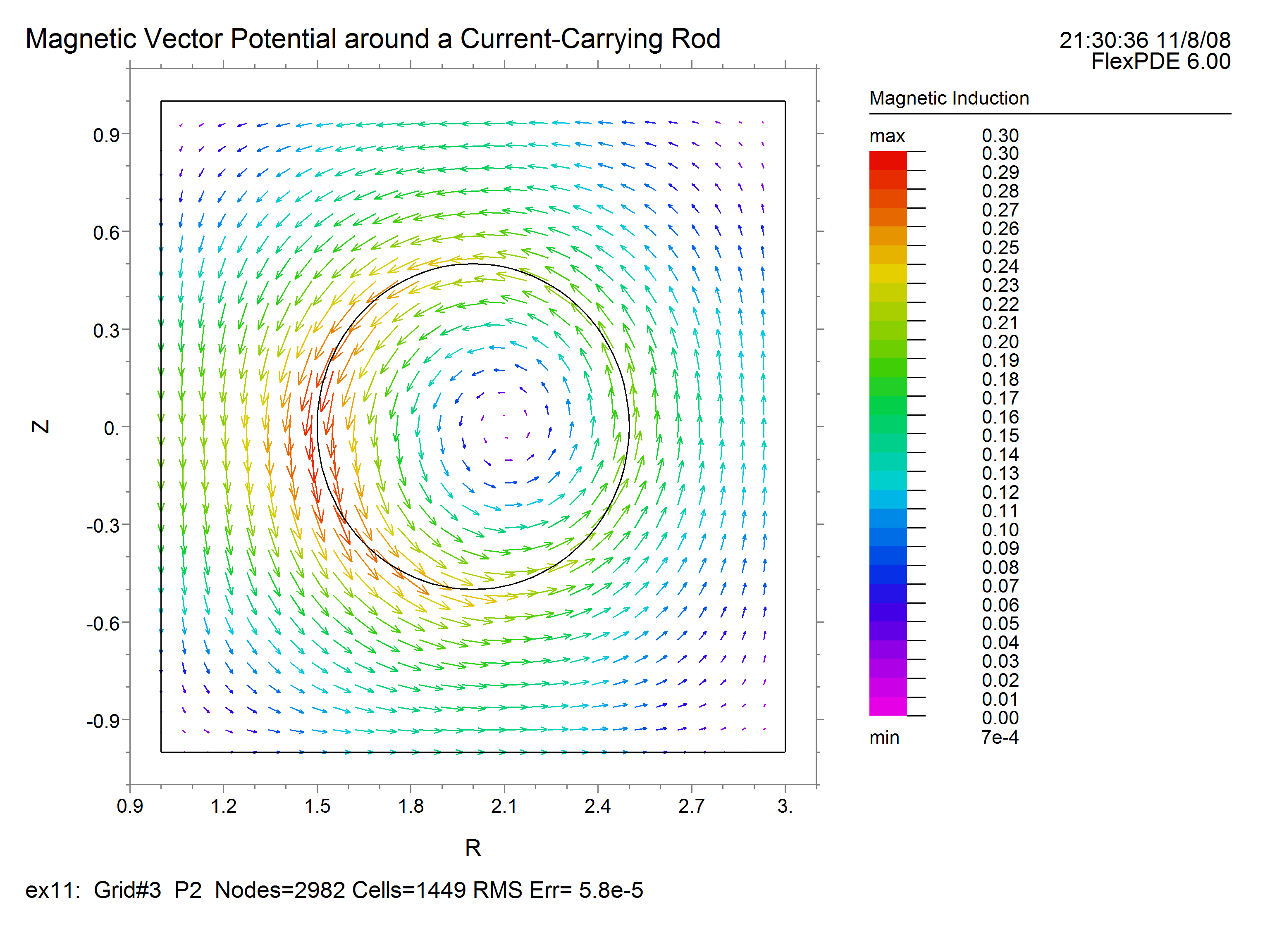
VECTOR(CURL(A)) as "Magnetic Induction"

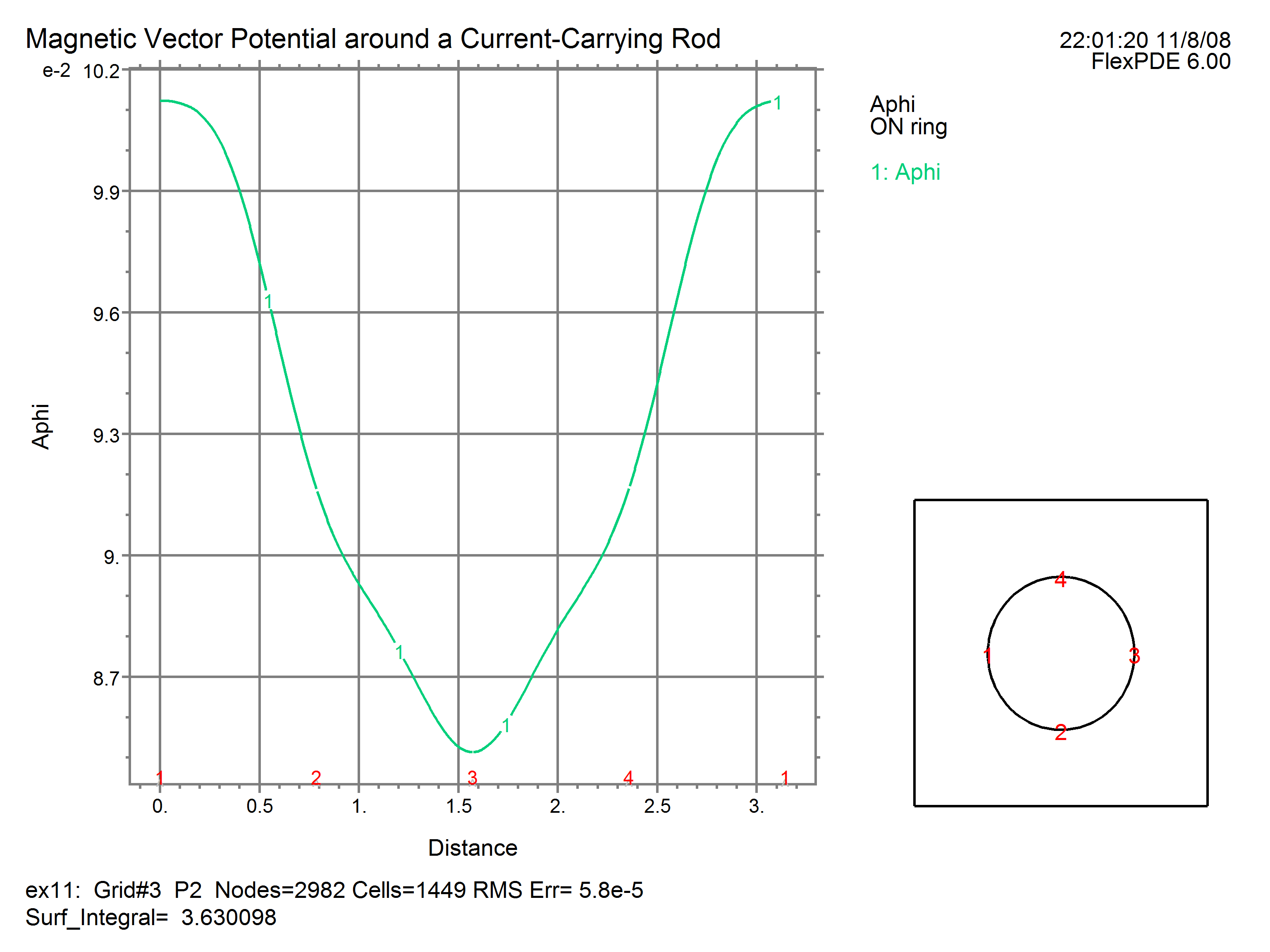
ELEVATION(Aphi) ON 'ring'

END

 

The resulting plots are: