|
<< Click to Display Table of Contents >> 1d_lagrangian_shock |
  
|
|
<< Click to Display Table of Contents >> 1d_lagrangian_shock |
  
|
{ 1D_LAGRANGIAN_SHOCK.PDE
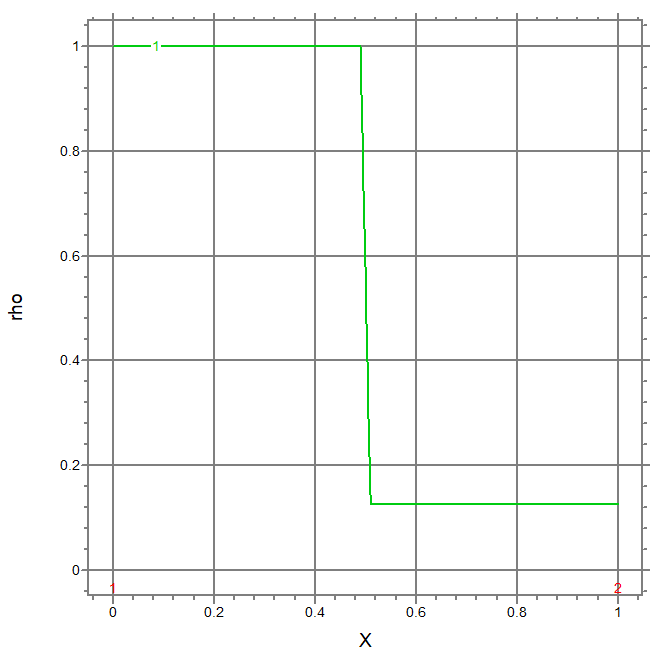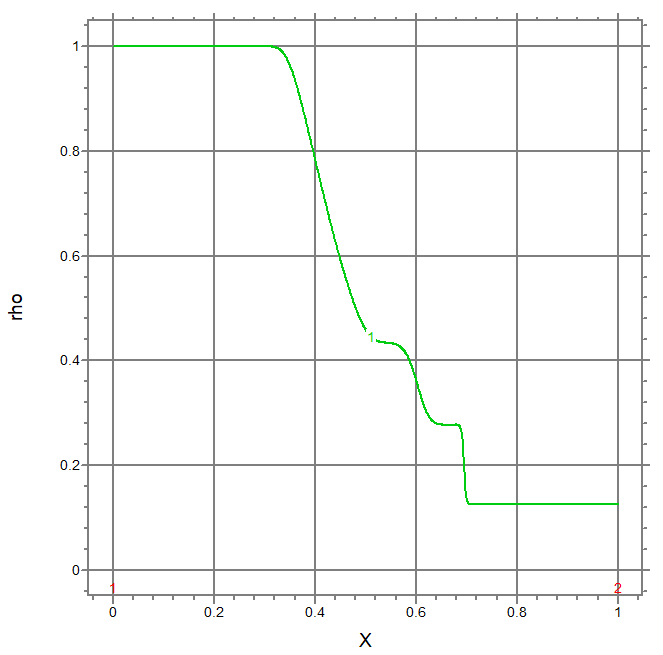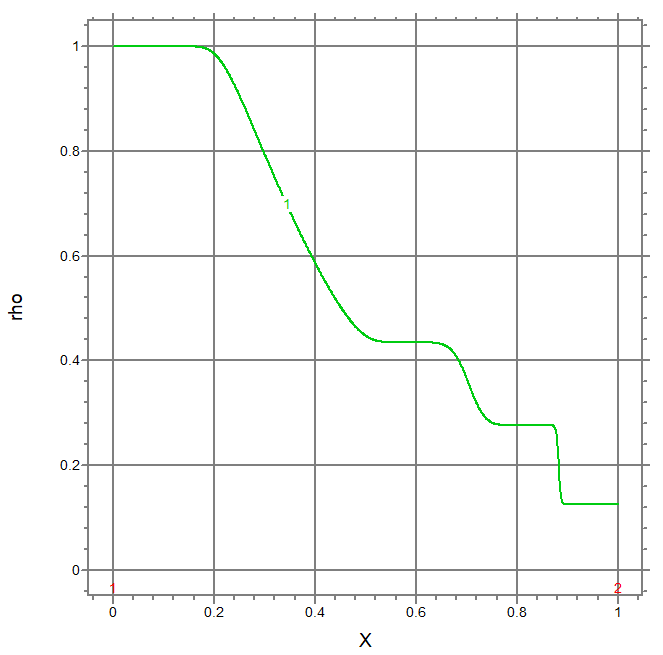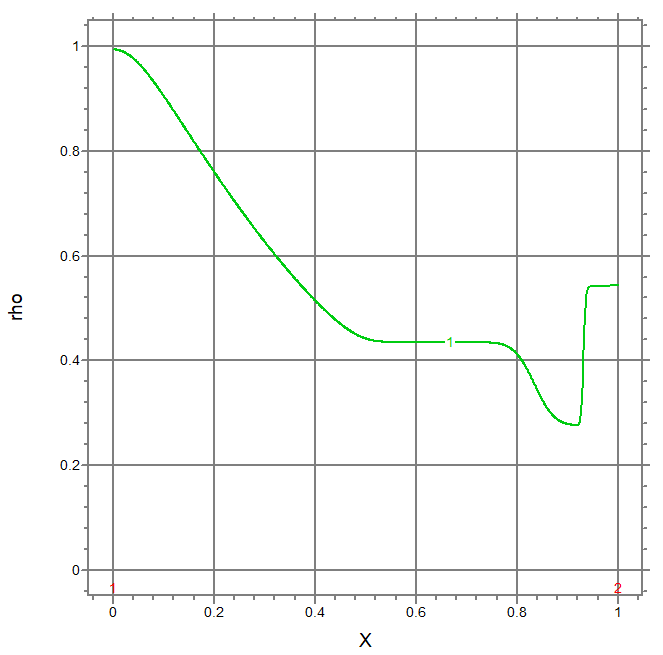
This example solves Sod's shock tube problem on a 1D moving mesh.
Mesh nodes are given the local fluid velocity, so the model is fully Lagrangian.
See 1D_EULERIAN_SHOCK.PDE for an Eulerian model of the same problem.
Ref: G.A. Sod, "A Survey of Several Finite Difference Methods for Systems of
Nonlinear Hyperbolic Conservation Laws", J. Comp. Phys. 27, 1-31 (1978)
See also Kershaw, Prasad and Shaw, "3D Unstructured ALE Hydrodynamics with the
Upwind Discontinuous Finite Element Method", UCRL-JC-122104, Sept 1995.
}
TITLE "Sod's Shock Tube Problem - Lagrangian"
COORDINATES
cartesian1
SELECT
ngrid = 100 { increase the grid density }
regrid = off { disable the adaptive mesh refinement }
errlim = 1e-4 { lower the error limit }
VARIABLES
rho(1)
u(1)
P(1)
xm=move(x)
DEFINITIONS
len = 1
gamma = 1.4
smeardist = 0.001 { a damping term to kill unwanted oscillations }
eps = sqrt(gamma)*smeardist { ~ cspeed*dist }
v = 0
rho0 = 1.0 - 0.875*uramp(x-0.49, x-0.51)
p0 = 1.0 - 0.9*uramp(x-0.49, x-0.51)
INITIAL VALUES
rho = rho0
u = 0
P = p0
EULERIAN EQUATIONS
{ equations are stated as appropriate to the Eulerian (lab) frame.
FlexPDE will convert to Lagrangian form for moving mesh }
rho: dt(rho) + u*dx(rho) + rho*dx(u) = eps*dxx(rho)
u: dt(u) + u*dx(u) + dx(P)/rho = eps*dxx(u)
P: dt(P) + u*dx(P) + gamma*P*dx(u) = eps*dxx(P)
xm: dt(xm) = u
BOUNDARIES
REGION 1
START(0) point value(u)=0 point value(xm)=0
line to (len) point value(u)=0 point value(xm)=len
TIME 0 TO 0.375
MONITORS
for cycle=5
elevation(rho) from(0) to (len) range (0,1)
elevation(u) from(0) to (len) range (0,1)
elevation(P) from(0) to (len) range (0,1)
PLOTS
for t=0 by 0.02 to 0.143, 0.16 by 0.02 to 0.375
elevation(rho) from(0) to (len) range (0,1)
elevation(u) from(0) to (len) range (0,1)
elevation(P) from(0) to (len) range (0,1)
grid(x)
END