In many cases, the waveguide under analysis consists of a metal casing, either empty or filled homogeneously with an isotropic dielectric.  In these cases, the analysis can be simplified.

Eq. (3.3) can be expanded using (3.5) and rearranged to express the transverse x and y components in terms of the axial z components and .
(3.6)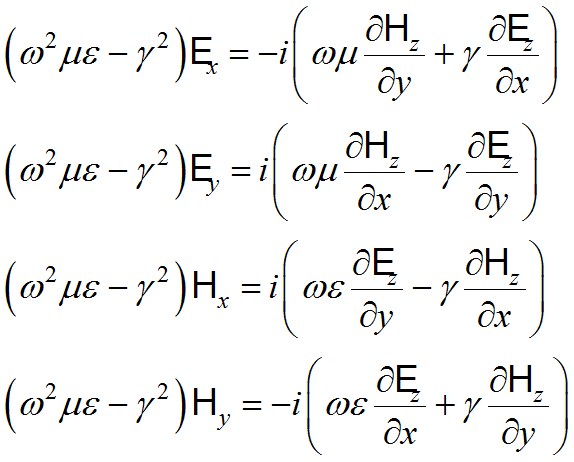    

The in the right hand side corresponds to a phase shift of in the expansion (3.1).

Applying, the divergence equations of (3.3) become
(3.7)     ,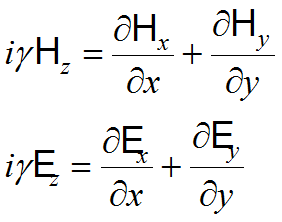

so  the z component equations of (3.4) are
(3.8)     .

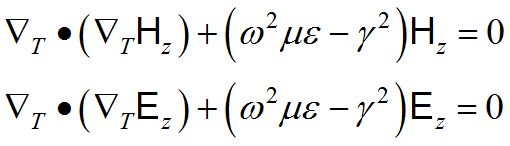
These are eigenvalue equations in and , and the values of for which solutions exist constitute the propagation constants of the unattenuated propagation modes that can be supported in the guide under analysis.  For any eigenvalue, there are an infinite number of combinations of which can excite this mode, and the exact determination will depend on the materials and the driving frequency.