<< Click to Display Table of Contents >> Navigation:  Technical Notes > Applications in Electromagnetics > Waveguides

A waveguide is any of several kinds of structure intended to direct the propagation of high-frequency electromagnetic energy along specific paths.  While the analysis of bends and terminations in such a system is an essentially three-dimensional problem, the propagation in long straight segments of the guide can be reduced to a two-dimensional analysis.  In this case, we assume that the guide is of uniform cross-section in the (X,Y) plane, unvarying in the Z-dimension of the propagation direction.  In this configuration, we can make the assumption that the fields inside the guide may be represented as a sinusoidal oscillation in time and space, and write

(3.1)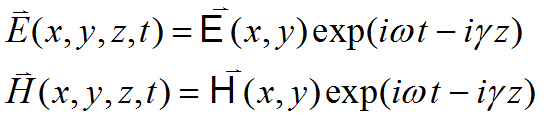    

It is easy to see that these expressions describe a traveling wave, since the imaginary exponential generates sines and cosines, and the value of the exponential will be the same wherever .  A purely real implies an unattenuated propagating mode with wavelength along the z direction.

We start from the time-dependent form of Maxwell’s equations

(3.2)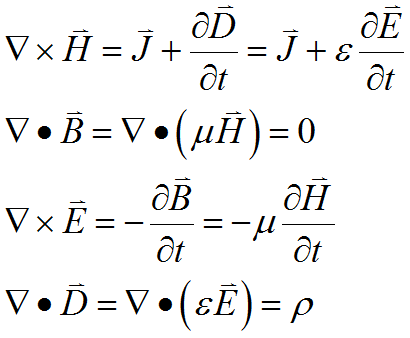    

 

Assume then that and , and apply (3.1) :

(3.3)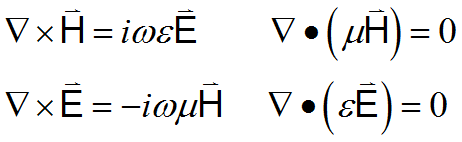      

Taking the curl of each curl equation in (3.3) and substituting gives

(3.4)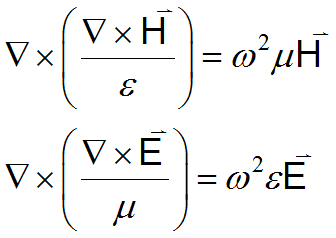  

In view of (3.1), we can write

(3.5)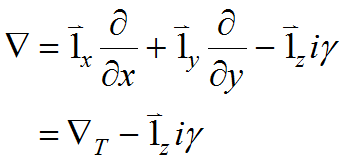  

with denoting the operator in the transverse plane.