|
<< Click to Display Table of Contents >> 2d_blob_velocity |
  
|
|
<< Click to Display Table of Contents >> 2d_blob_velocity |
  
|
{ 2D_BLOB_VELOCITY.PDE
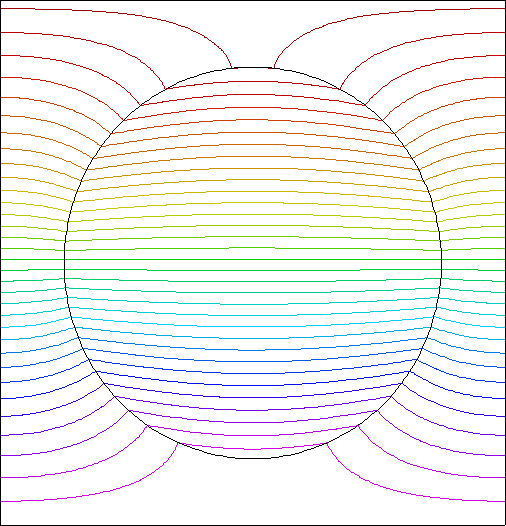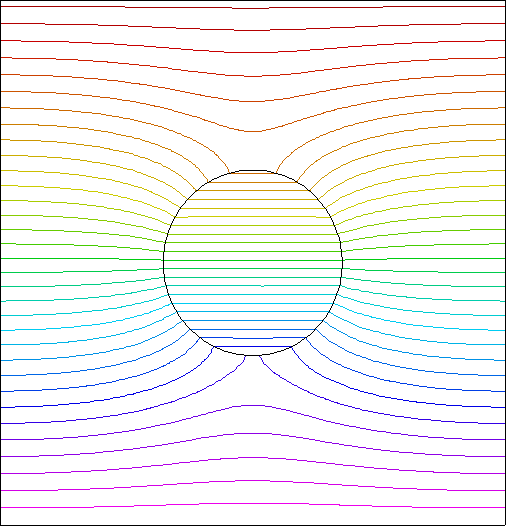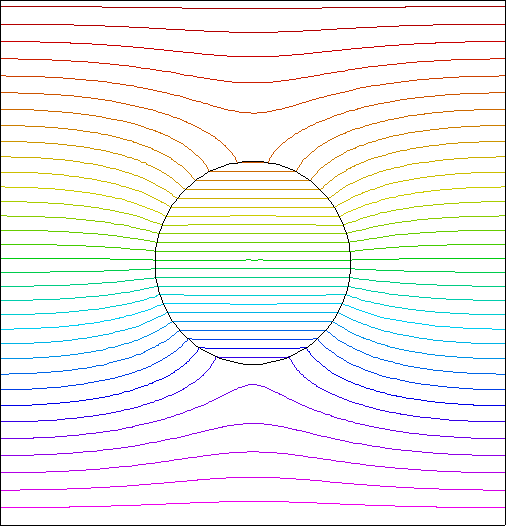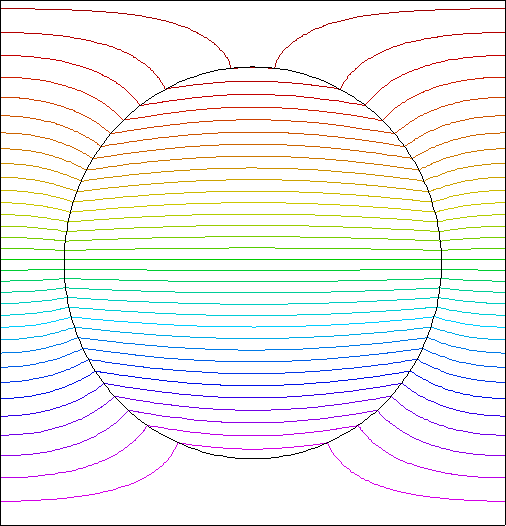
This problem illustrates moving meshes in 2D.
A circular boundary shrinks and grows sinusoidally in time.
The mesh coordinates are solved by reference to a mesh velocity variable.
See 2D_BLOB_POSITION.PDE for a version that uses no mesh velocity variables.
}

TITLE 'Pulsating circle in 2D - velocity specification'
COORDINATES
cartesian2
VARIABLES
Phi { the temperature }
Xm = MOVE(x) { surrogate X }
Ym = MOVE(y) { surrogate Y }
Um(0.1) { mesh x-velocity }
Vm(0.1) { mesh y-velocity }
DEFINITIONS
K = 1 { default conductivity }
R0 = 0.75 { initial blob radius }
INITIAL VALUES
Phi = (y+1)/2
EULERIAN EQUATIONS
Phi: Div(-k*grad(phi)) = 0
Xm: dt(Xm) = Um
Ym: dt(Ym) = Vm
Um: div(grad(Um)) = 0
Vm: div(grad(Vm)) = 0
BOUNDARIES
REGION 1 'box'
START(-1,-1)
VALUE(Phi)=0
VELOCITY(Xm)=0 VELOCITY(Ym)=0
VALUE(Um)=0 VALUE(Vm)=0
LINE TO (1,-1)
NATURAL(Phi)=0
LINE TO (1,1)
VALUE(Phi)=1
LINE TO (-1,1)
NATURAL(Phi)=0
LINE TO CLOSE
REGION 2 'blob' { the embedded blob }
k = 0.001
START 'ring' (R0,0)
VELOCITY(Xm) = Um
VELOCITY(Ym) = Vm
VALUE(Um) = -0.25*sin(t)*x/r
VALUE(Vm) = -0.25*sin(t)*y/r
ARC(CENTER=0,0) ANGLE=360 TO CLOSE
TIME 0 TO 2*pi
MONITORS
for cycle=1
grid(x,y)
contour(phi)
PLOTS
FOR T = 0 BY pi/20 TO 2*pi
GRID(x,y)
CONTOUR(Phi) notags nominmax
VECTOR(-k*grad(Phi))
CONTOUR(magnitude(Um,Vm))
VECTOR(Um,Vm) fixed range(0,0.25)
ELEVATION(Phi) FROM (0,-1) to (0,1)
ELEVATION(Normal(-k*grad(Phi))) ON 'ring'
END