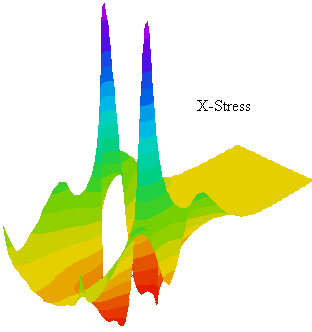
This problem shows the deformation of a tension bar with a hole. FlexPDE solves two simultaneous Partial Differential Equations for the X- and Y- displacements within the bar.
dx(Sx) + dy(Txy) + Fx = 0
dx(Txy) + dy(Sy) + Fy = 0
where Sx and Sy are the stresses in the X- and Y- directions, Txy is the shear stress, and Fx and Fy are the body forces in the X- and Y- directions.
Sx = C11*dx(U) + C12*dy(V) + C13*[dy(U) + dx(V)]
Sy = C12*dx(U) + C22*dy(V) + C23*(dy(U) + dx(V))
Txy = C13*dx(U) + C23*dy(V) + C33*(dy(U) + dx(V))
Here the Cnn are the constitutive relations of the material.
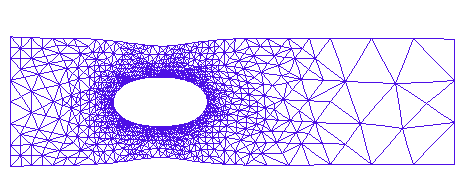
The Final Adaptively Refined Grid
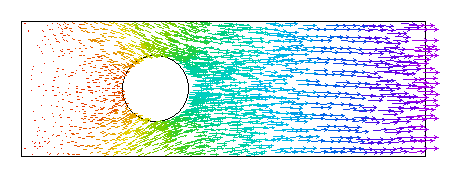
The Vector Displacement Field
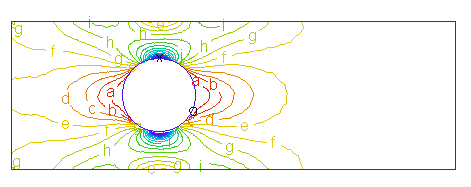
The X-Directed Stress