|
<< Click to Display Table of Contents >> Rotated_heat_ring |
  
|
|
<< Click to Display Table of Contents >> Rotated_heat_ring |
  
|
{ ROTATED_HEAT_RING.PDE
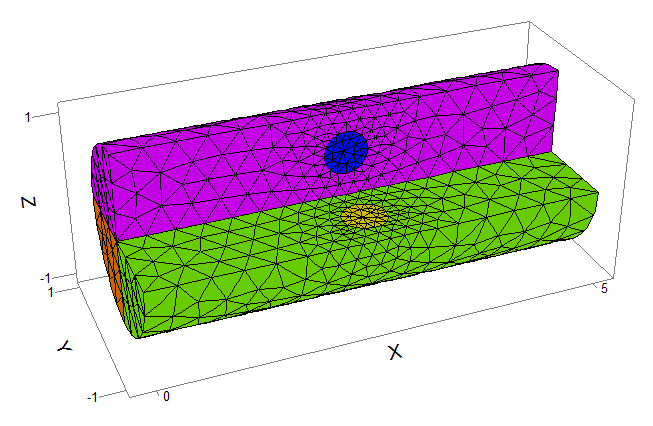
This example illustrates Extrusion in angle (Rotation), by which a 2D axisymmetric model may be easily converted to 3D.
A rod of conductive material of unit radius and "long" units length
has an imbedded heated ring.
The (x,y) layout is rotated 360 degrees in azimuthal angle, and the extrusion is
divided into four segments (layers) with differing source values.
}

title
"Rotated Heat Ring"
coordinates
xcylinder3
select
automesh= off
ngrid=20
painted
errlim=1e-3
variables
temp(threshold=10)
definitions
k = 0.85 { thermal conductivity }
cp = 1 { heat capacity }
long = 5
H = 2.0-sin(phi) ! 0.4 { free convection boundary coupling - ANGLE DEPENDENT }
Ta = 25 { ambient temperature }
A = 4500 { amplitude }
phimax = 360 degrees
source = A*r
initial value
temp = Ta
equations
temp : div(k*grad(temp)) + source = 0
Rotation
surface phi=0
layer "one"
surface phi=phimax/4
layer "two"
surface phi=phimax/2
layer "three"
surface phi=3*phimax/4
layer "four"
surface phi=phimax
boundaries
region 1
A = 0 { no source in outer material }
start(0,0)
natural(temp) = 0 line to (long,0) { axis }
value(temp) = Ta line to (long,1) { end plane }
value(temp)=Ta line to (2*long/3,1) { fix surface temp at Ta on end third }
natural(temp) = -H*(temp - Ta) line to (long/3,1) { convection cooling on center third }
value(temp)=Ta line to (0,1) { fix surface temp at Ta on first third }
value(temp) = Ta line to close { end plane }
{ the heating ring }
limited region 2
layer 1 A=4500 { first quadrant source }
layer 2 A=1000 { second quadrant source }
layer 3 A=3000 { firthirdst quadrant source }
layer 4 A=0 { fourth quadrant source }
start(long/2,1/2-1/4) { ring has circular cross-section }
arc(center=long/2,1/2) angle=360
plots
grid(x,y,z) on layers "one", "three", "four" paintregions
glgrid(x,y,z) on layers "one", "three", "four" paintregions
glcontour(temp) as "Rotatable surface temp"
glcontour(temp) on region 2 nolines as "Rotatable heat ring temp"
glcontour(temp) on region 2 on layer 2 as "Rotatable heat ring temp in second quadrant"
glcontour(-H*(temp-Ta)) as "Surface Loss H*(Temp-Ta)" report("H = 2.0-sin(phi)")
elevation(temp) from (0,0) to (long,0) as "Axis Temp" { trace temp on axis }
contour(temp) on x=long/2 as "Temp cros-section"
contour(temp) on phi = phimax/3 as "Temp slice at phi=120"
contour(magnitude(grad(temp))) on x=long/2 as "Cartesian Gradient on cross-section"
contour(magnitude(vector(dx(temp),dr(temp),dphi(temp)/r))) on x=long/2 as "Polar-Coordinate Gradient on cross-section"
contour(magnitude(grad(temp))) on phi=phimax/2 as "Gradient slice at phi=180"
contour(magnitude(grad(temp))) on phi=0 as "Gradient slice at phi=0"
contour(k*dr(temp)) on x=long/2 as "Radial flux"
contour(dr(temp)) on x=long/2 as "Radial derivative"
contour(drr(temp)) on x=long/2 as "Radial curvature"
contour(dphi(temp)/r) on x=long/2 as "Azimuthal derivative"
vector(-grad(temp)) on x=long/2 as "Cartesian gradient on cross-section"
contour(source) on x=long/2
grid(y,z) on x=long/2 paintregions as "Grid cross-section by region"
grid(y,z) on x=long/2 paintmaterials as "Grid cross-section by material"
grid(x,y) on phi=0 as "Grid on X,Y slice at phi=0"
grid(x,r) on phi=0 as "Grid on X,R slice at phi=0"
contour(source) on phi = pi/4
contour(source) on phi = 3*pi/4
summary
report(integral(source))
report(sintegral(-k*normal(grad(temp))))
end