Technical Notes > How FlexPDE Works

1. The Finite Element Model1

The modeling technique used in FlexPDE is a form of Finite Element Analysis.

a)The domain of interest is divided into a large number of small patches or elements (line segments in 1D, triangles in 2D and tetrahedra in 3D).

b)In each element, a modeled variable is approximated by a polynomial approximation in space. eg where each is a shape function2 within the element and the are the coefficients of the approximation.

c)The shape functions used in FlexPDE are heirarchical3, in that the lowest order is a linear interpolation among the vertex values. To this fundamental interpolation may be added a quadratic supplement, and possibly a cubic supplement.

d)The shape functions used in FlexPDE are by default cubic in space. The approximation order is controllable using the selectors order=1,2 or 3 (or linear, quadratic and cubic).

2. Galerkin Weighted Residuals4

a)Given a Partial Differential Equation, FlexPDE automatically generates a Galerkin Weighted Residual discretisation of the PDE. This is done by multiplying the PDE by each of the shape functions and integrating over each cell.

b)For example, the PDE becomes (in 1D) the set for each j. Inserting the expansion rule 1(b), this becomes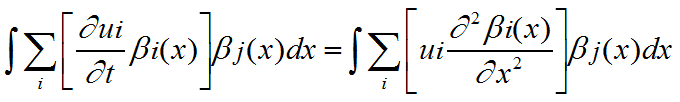

c)Second-order derivatives are reduced in order by applying Integration by Parts5 (equivalent to the Divergence Theorem in the case of a divergence operator or the Curl Theorem in the case of a curl operator). This produces 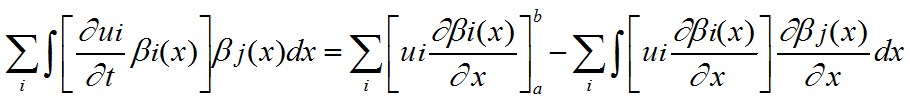for each j. The products of shape functions can be pre-computed, so that we can write

d)The boundary terms introduced by this procedure imply the continuity of flux (e.g. the argument of the divergence operator) across element and material interfaces.

e)The integrals involving shape functions can be precomputed. We use quadrature rules together with values of e.g. at each quadrature point q.

f)This process results in a set of residual equations which can be denoted by . It is the coupled set of these residual equations for variables that we must solve to generate a model solution.

g)Petrov-Galerkin Stabilization6,7
FlexPDE automatically applies Petrov-Galerkin weighting to equatons when advection terms are present. This scheme adds a secondary weighting term to the standard weighting .

3. The Solution Method

There are several different cases that arise when solving the systems generated in 2(c). Is the problem linear or non-linear? Is it time-dependent or steady-state? In all cases, we start by differentiating each equation with respect to all the expansion coefficients, resulting in an equation system which can be solved for modifications that must be applied to the variables u and v. Each entry in this diagram represents an entire assembly of equations and variables for each shape function in each cell of the Finite Element assembly. This can result in matrices of thousands or even millions of entries. All the methods used in FlexPDE are fully implicit and require matrix inversion to solve for new values. In a fully general system like FlexPDE, this is necessary to maintain stability and accuracy.

a)Linear Steady-State Systems
In the simplest case, the terms are independent of the variables u, v... and can be solved directly. FlexPDE uses an iteration on residuals to repeat the solution until the accuracy is within tolerance (because Preconditioned systems described below find a solution in a different space than the actual solution space).

b)Nonlinear Steady_State Systems
If the terms contain dependencies on the system variables u, v..., then we must use a Newton’s method to repeatedly compute the matrix and right-hand side terms and apply the indicated changes until convergence is achieved. FlexPDE uses a method of line searches and backtracking8 to prevent divergent iterations.

c)Time-Dependent Systems
If the equations contain time derivatives, we will have terms arising from the part of equations 2(f). In this case, we must track the time evolution of the coefficients . FlexPDE uses a selectable-order Backward Difference Formulation9 to advance the variables in time. This is similar to Gear’s method, and is adapted to stiff systems. The default method in FlexPDE is quadratic in time, but a first-order method is used during start-up.
i) In linear systems, each time step may be computed once.
ii) In nonlinear systems, each time step may require multiple Newton iterations. In FlexPDE this is controlled by the selectors PREFER_SPEED and PREFER_STABILITY, q.v.. In the former case, one Newton step is computed for each time step, on the assumption that the solution will not vary much over the step. In the latter case, a maximum of 3 Newton steps are allowed in each time step. This number con be controlled with the NEWTON selector.

4. Solving the Matrix Systems

FlexPDE uses Conjugate-Gradient iteration extensively in solving the matrix equations (3). This is because the matrices generated by element-to-element coupling are very sparse and very large. The particular variety of CG iteration used depends on the characteristics of the matrix. There are many variations of CG iteration available, and FlexPDE has defaults but offers some selection of alternate methods.

a)a) Conjugate Gradient solvers

i) Symmetric systems, as generated by diffusion-type equations, use an Orthomin system10,11

ii) Nonsymmetric systems require bi-orthogonalization, and FlexPDE uses the Lanczos method12,13. This method solves the double system . is arbitrary.

iii) Some nonsymmetric systems require a different technique, and FlexPDE offers a method due to Vandenberg that solves the system in the form 14.

iv) A changing number of other CG methods are available in FlexPDE, and are being evaluated for efficacy. At present, those listed have been the most reliable.

b)b) Preconditioning
In all cases, FlexPDE uses a preconditioner to improve the convergence of the Conjugate-Gradient iteration. The goal of this operation is to reduce the range of eigenvalues of the iteration matrix to less than one.
i) Symmetric matrices by default use an Incomplete Choleski Decomposition15. If the incomplete decomposition is possible, then the system solved is and , where L is the lower triangular Incomplete Choleski decomposition of A.
If the Incomplete Choleski decomposition fails, then symmetric systems default to , where B is the matrix of diagonal blocks coupling the variables of each coefficient.
ii) For nonsymmetric systems, the system solved is , where B is the matrix of diagonal blocks as in (i).

c)A direct solver using the Intel Math Kernel Library16 is available for small systems, using the control word DIRECT. At present, this option is limited to 10,000 matrix rows.

5. Automatic Mesh Refinement

FlexPDE monitors the accuracy of the Finite Element approximation and corrects the mesh density to get higher resolution in the areas of the domain where the solution is changing rapidly and accuracy is compromised. Beginning in version 7, FlexPDE estimates the solution accuracy simply by monitoring the contribution of the highest-order term to the overall solution in each cell (in order=1 solutions, a multi-cell method is used to estimate second-order contributions). By splitting any cell in which the highest-order contribution is large, we keep the mesh density sufficiently high to achieve accuracy.

6. Moving Meshes

FlexPDE supports Finite Element meshes that move in time. In this case, surrogate system variables are declared in order to couple the main variables to changes in the node positions. The residual equations and Jacobian matrices must then be adjusted for the fact that the cell volumes and interpolation coefficients are changing in time. These additional terms are added to the system diagrammed in (3).

1. There are many references describing Finite Element methods, see for example Zienkiewicz, O.C. and R.L. Taylor, “The Finite Element Method, Fifth Edition, Volume 1: the Basis” 2000

2. Zienkiewicz and Taylor, chapter 8.

3. Zienkiewicz and Taylor, section 8.16

4. Zienliewicz and Taylor, chapter 3.

5. Zienkiewicz and Taylor, Appendix G

6. Sert, C., ME582 “Finite Element Analysis in Thermofluids” http://users.metu.edu.tr/csert/me582/ME582%20Ch%2006.pdf

7. Zienkiewicz, O.C. and R.L. Taylor, “The Finite Element Method, Fifth Edition, Volume 3: Fluid Dynamics” ( 2000) section 2.3.2

8. For example, Numerical Recipes in C++, second edition, section 9.7

9. For example, Ascher and Petzold, “Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations” (1998) section 5.1.2

10. Young, D.M. and Kang C. Jea, “On the Simplification of Generalized Conjugate-Gradient Methods for Nonsymmetrizable Linear Systems” Linear Algebra and its Applications 52/53:399 (1983)

11. Saad, Yousef, “Iterative Methods for Sparse Linear Systems”, second edition (2003), section 6.9

12. Young and Jea, op cit.

13. Saad, op cit, section 7.1

14. T.K. Sarkar, “Application of Conjugate Gradient Method to Electromagnetics and Signal Analysis” , Elsevier (1991), chapter 2

15. Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Johns Hopkins, Section 10.3.2.

16. https://www.intel.com/content/www/us/en/developer/tools/oneapi/onemkl.html