<< Click to Display Table of Contents >> Navigation:  Sample Problems > Usage > Periodicity > 2d_wave_propagation

{

  2D_WAVE_PROPAGATION.PDE

 

  This test shows a wave pattern propagating across a square, with periodic boundaries at the edges.

  It demonstrates that the Periodic boundary maintains solution integrity with time dependence.

}

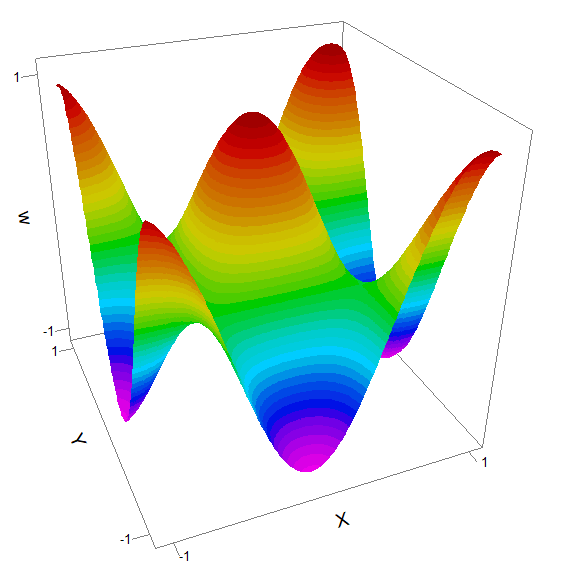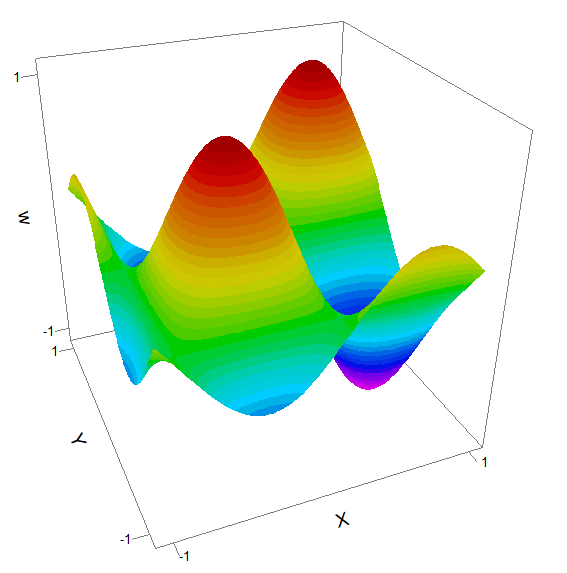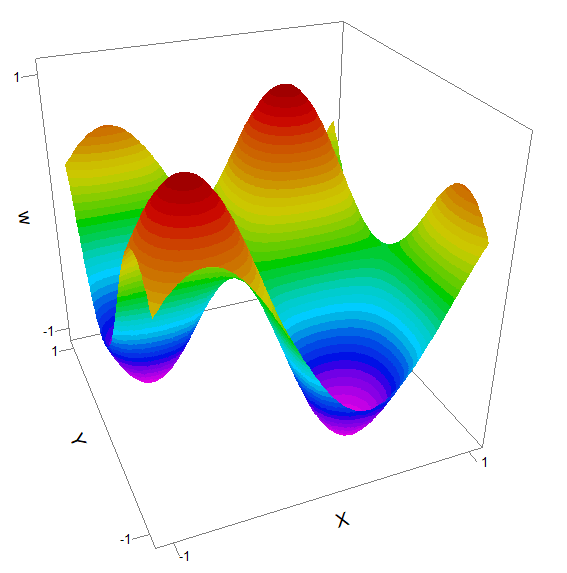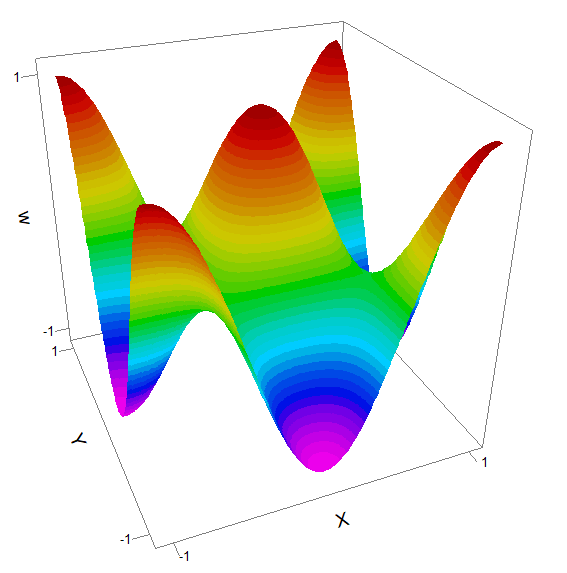
TITLE

      '2D wave propagation '

 

COORDINATES

       CARTESIAN2

 

VARIABLES

       w(0)

 

select

   errlim = 1e-4

 

DEFINITIONS

   tend=4.0

   u = 1

   v = 1

 

INITIAL VALUES

       w=COS(PI*x)*COS(PI*y)

       

EQUATIONS

      w : DT(w) - u*DX(w) - v*DY(w) = 0

       

BOUNDARIES

      REGION 1

    { Periodic bottom boundary }

    start(-1,-1)

    periodic(x,y+2) line to (1,-1)

 

    { Periodic right boundary }

    periodic(x-2,y) line to (1,1)

 

    { Image of periodic bottom boundary }

    line to  (-1,1)

 

    { Image of periodic right boundary }

    line to close

 

 

 

TIME 0 TO tend

 

PLOTS

      FOR t=0 BY tend/50 to tend

              surface(w)

              surface(dx(w))

              surface(dy(w))

 

END