<< Click to Display Table of Contents >> Navigation:  User Guide > Addressing More Difficult Problems > Discontinuous Variables > Using JUMP in problems with many variables

An expression JUMP(V) may appear in any boundary condition statement  on a boundary for which the argument variable V has been given a CONTACT boundary condition.  

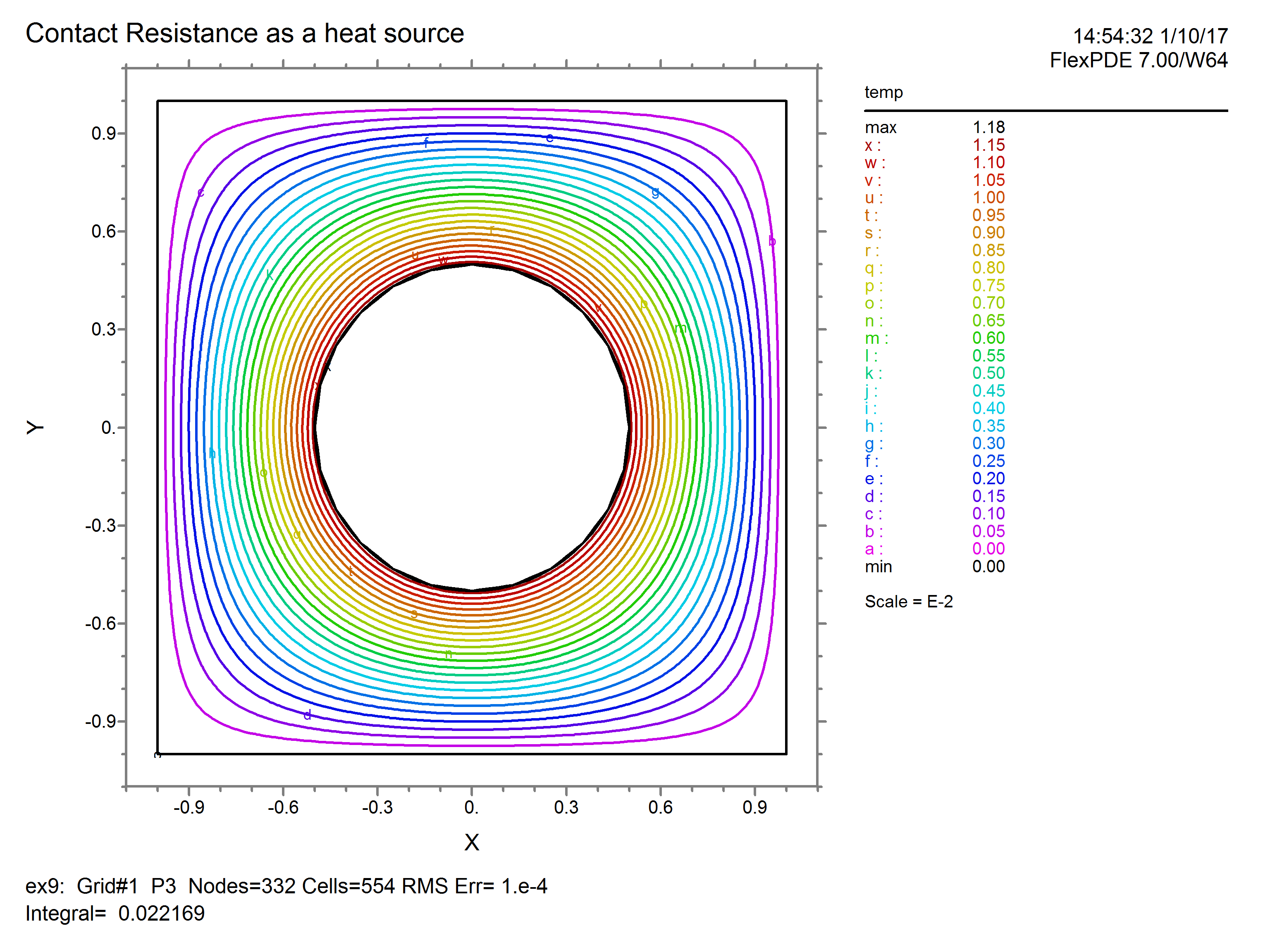
In an electrical resistance case, for example, the voltage undergoes a jump across a contact resistance, and the current through this contact is a source of heat for a heatflow equation.  The following example, though not strictly realizable physically, diagrams the technique.  Notice that the JUMP of Phi appears as a source term in the Natural boundary condition for Temp. Phi, having appeared in a CONTACT boundary condition definition, is stored as a double-valued quantity, whose JUMP is available to the boundary condition for Temp. Temp, which does not appear in a CONTACT boundary condition statement, is a single-valued variable at the interface.

TITLE 'Contact Resistance as a heat source'

VARIABLES

Phi                { the voltage }

Temp                { the temperature }

DEFINITIONS

Kd = 1                { dielectric constant }

Kt = 1                { thermal conductivity }

R = 0.5                { blob radius }

Q = 0                { space charge density }

Res = 0.5        { contact resistance }

EQUATIONS

Phi:        Div(-kd*grad(phi)) = Q

Temp:        Div(-kt*grad(temp) = 0

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0        { grounded outer walls }

VALUE(Temp)=0        { cold outer walls }

LINE TO (1,-1) TO (1,1) TO (-1,1) TO CLOSE

REGION 2        'blob'        { the embedded blob }

Q = 1        { space charge in the blob }

START 'ring' (R,0)

CONTACT(phi) = -JUMP(phi)/Res

{ the heat source is the voltage difference times the current }

NATURAL(temp) = -JUMP(Phi)^2/Res

ARC(CENTER=0,0) ANGLE=360 TO CLOSE

PLOTS

CONTOUR(Phi)        SURFACE(Phi)

CONTOUR(temp)        SURFACE(temp)

END

 

The temperature shows the effect of the surface source: