<< Click to Display Table of Contents >> Navigation:  Technical Notes > Applications in Electromagnetics > Magnetostatics

From Maxwell’s equations in a steady-state form we have

(2.1)

         

         

where is the magnetic field intensity, is the magnetic induction, is the magnetic permeability and is the current density.

The conditions required by Maxwell’s equations at a material interface are

(2.2)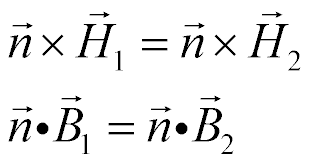    

It is sometimes fruitful to use the magnetic field quantities directly as variables in a model.  However, eq. (2.2) shows that the tangential components of are continuous across an interface, while the normal components of are continuous.

The finite element method used by FlexPDE has a single value of each variable on an interface, and therefore requires that the quantities chosen for system variables must be continuous across the interface.  In special cases, it may be possible to choose components of or which satisfy this continuity requirement.  We could, for example model in a problem where material interfaces are normal to .  In the general case, however, meeting the continuity requirements can be impossible.

It is common in Magnetostatics to use instead of the field quantities the magnetic vector potential , defined as

(2.3)     .

 

This definition automatically enforces .  Furthermore, can be shown to be continuous everywhere in the domain, and can represent the conditions (2.2) correctly.

can be derived from Ampere’s Law, and shown to be the integrated effect at each point of all the current loops active in the domain.  In this derivation, will have components parallel to the components of , so that it can be determined a priori which components of must be represented.

Eq. (2.3) alone is not sufficient to uniquely define .  It must be supplemented by a definition of to be unique.  This definition (the “gauge condition”) is usually taken to be (“Coulomb gauge”), a definition consistent with the derivation of from Ampere’s Law.  Other definitions are useful in some applications.  It is not important what the qauge condition is; in all cases, and therefore the field quantities, remain the same.

Combining eq. (2.1) with (2.3) gives

(2.4)    

In cases with multiple materials, where can take on different values, it is important to keep the inside the curl operator, because it is the integration of this term by parts that gives the correct jump conditions at the material interface.

Applying eq. (0.5) we have

(2.5)     ,

so that the Natural boundary condition defines on external boundaries, and is assumed continuous across internal boundaries, consistent with Maxwell’s equations.